| Search for content and authors |
Dyfrakcyjne badania mikrostruktury polikryształów nanometrowych poddawanych działaniu wysokiego ciśnienia |
| Roman Pielaszek |
|
Polish Academy of Sciences, High Pressure Research Center (UNIPRESS), Sokolowska 29/37, Warszawa 01-142, Poland |
| Abstract |
Niniejsza rozprawa poświęcona jest dyfrakcji promieniowania rentgenowskiego na kryształach nanometrowych. Zostały w niej omówione zarówno oryginalne wyniki doświadczalne jak też nowe podejście teoretyczne wiążące mikrostrukturę nanokryształów z natężeniem rozpraszanego promieniowania rentgenowskiego. Zaproponowane przez autora metody badawcze stosują się do analizy rozpraszania rentgenowskiego na polikryształach submikronowych o dowolnej strukturze krystalicznej. W tej pracy wykorzystano je do opisu i badania nanokryształów o strukturze najgęstszego upakowania takich jak węglik krzemu, diament oraz azotek galu. Motywacja. Polikryształy i ceramiki nanometrowe wykonane z materiałów supertwardych, takich jak węglik krzemu i diament łączą w sobie odporność mechaniczną tych substancji z dodakowymi zaletami, będącymi efektem nanometrowych rozmiarów ziaren. Należą do nich duża homogeniczność (skutek małego rozmiaru ziaren), zwiększona plastyczność (skutek dyfuzji na granicach ziaren) i odporność na pękanie (skutek zatrzymywania dyslokacji na granicach ziaren). W Centrum Badań Wysokociśnieniowych PAN prowadzone są prace nad otrzymaniem nowych rodzajów ceramik i materiałów kompozytowych zbudowanych z kryształów nanometrowych. Niezbędną częścią tych prac jest, opisana w tej rozprawie, ilościowa charakteryzacja mikrostruktury zarówno wyjściowych nanoproszków jak i ich spieków. Obok materiałów supertwardych, CBW PAN rozwija technologię półprzewodnikową opartą na azotku galu. Nanokryształy i ceramiki azotku galu są naturalnym kandydatem na materiał podłożowy dla produkowanych przez CBW PAN niebieskich laserów. Cel pracy. Celem pracy było opracowanie metody wyznaczania pełnego rozkładu wielkości ziaren polikryształów nanometrowych na podstawie dyfraktogramów proszkowych. Wymagało w szczególności:
Opracowanie nowego podejścia teoretycznego było konieczne ze względu na niezadowalający w przypadku polikryształów nanometrowych opis dyfrakcji w ramach kinematycznej teorii dyfrakcji w jej standardowej postaci, szeroko stosowanej w badaniach polikryształów mikrometrowych. Z doświadczeń dyfrakcyjnych prowadzonych na nanokryształach wiadomo, że znane od prawie stu lat metody analizy danych dyfrakcji proszkowej w większości nie stosują się, a w najlepszym razie są bardzo nieprecyzyjne w odniesieniu do granicznie małych, ale też przecież polikryształów nanometrowych. Próby zastosowania równania Scherrera do określenia rozmiaru kryształu czy metody Warrena-Averbacha do znalezienia rozkładu wielkości ziaren w proszku nie przynoszą rezultatów dających się pogodzić ani z posiadanym materiałem doświadczalnym ani z numerycznymi obliczeniami rozpraszania na nanokryształach opartymi na prawach pierwszych (ab initio). Po okresie doskonalenia metod doświadczalnych1 , właśnie owe “prawa pierwsze” stały się moim punktem odniesienia, a początkowo także praktyczną metodą badań nad mikrostrukturą nanoproszków [?][?]. Pozwoliły one poprawnie określać strukturę, dokładne rozmiary i uporządkowanie ziaren nanoproszków. Praca nad poprawą wydajności algorytmów obliczających rozpraszanie na coraz bardziej złożonych (i realistycznych) modelach proszków zaowocowała odczuwalnym przyspieszeniem tych obliczeń2 , ale przede wszystkim spostrzeżeniami o matematycznej naturze warunków brzegowych, które czynią dyfrakcję na nanokryształach odmienną od “klasycznej”. Trzeba powiedzieć, że bez natychmiastowego potwierdzania lub odrzucania roboczych hipotez możliwego przez połączenie obliczeń ab initio z mocą dzisiejszych komputerów, praca nad sformalizowaniem opisu dyfrakcji na nanokryształach nie mogłaby być podjęta. Metody stosowane dotychczas. Tradycyjna, nienanokrystaliczna, dyfrakcja proszkowa opisywana jest w oparciu o kinematyczną teorię dyfrakcji Lauego. Zakłada ona brak ugięć wielokrotnych oraz stałość absorpcji w krysztale. Założenia te są dobrze spełnione dla nanokryształów, mających zawsze formę proszków. Jednakże zasadnicze, interferencyjne równanie teorii kinematycznej (patrz np. wyrażenie (3⋅48) w pracy [?] lub (3.6) w pracy [?]) zostało wyprowadzone dla natężenia promieniowania rozproszonego na monokrysztale a więc przy założeniu (i) periodycznej struktury atomowej przyjmując ponadto (ii) prostopadłościenny kształt kryształu (lewa gałąź diagramu przedstawionego na rys. 1.1 na str. 11). Te dodatkowe założenia są w przypadku dyfrakcji proszkowej nieuzasadnione. Pomimo tego, równanie interferencyjne jest punktem wyjścia tradycyjnych metod analizy proszkowych danych dyfrakcyjnych, takich jak metoda Warrena-Averbacha lub metoda Scherrera. Na rys. 1.1 zestawiono najważniejsze metody analizy dyfrakcji promieniowania rentgenowskiego rozwinięte w ramach kinematycznej teorii dyfrakcji, zaznaczając ich wzajemne powiązania. Część diagramu zamknięta linią przerywaną stanowi oryginalny wkład oparty na zaproponowanym przez autora wzorze Debye’a dla kryształów - część ta została omówiona w rozdziale 2. 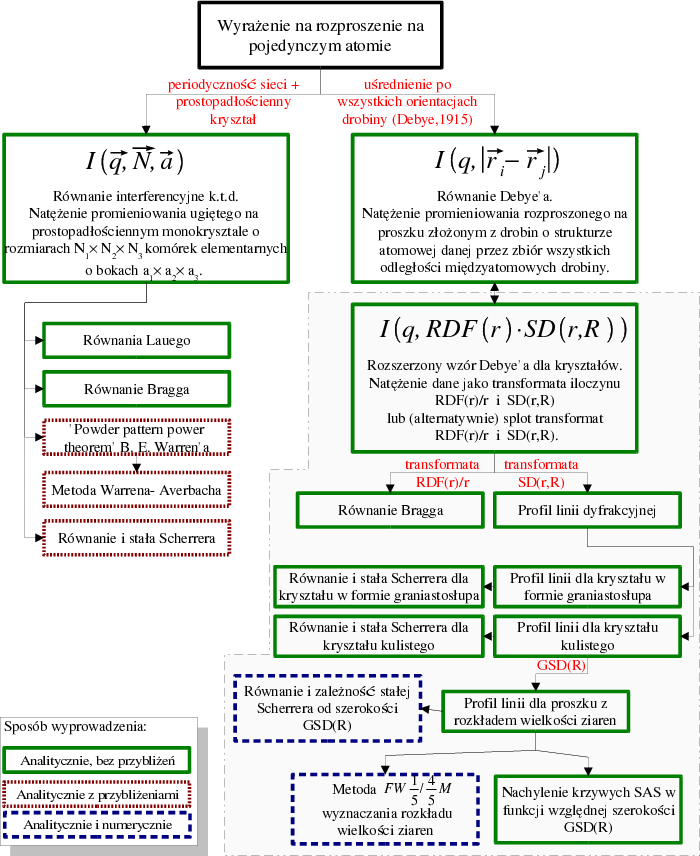 Rysunek 1.1: Kinematyczna teoria dyfrakcji (k.t.d.). Jej rdzeniem jest równanie interferencyjne (lewa gałąź). Rozwinięcie wzoru Debye’a (prawa gałąź) pozwala podać równania wiążące mikrostrukturę krystalitów i natężenie rozproszonego na nich promieniowania. Wyprowadzenia odpowiadające części diagramu zakreślonej linią przerywaną przedstawiono w rozdziale 2. Oznaczenia: RDF(r)-funkcja rozkładu radialnego; SD(r; R)-dystrybucja kształtu; GSD(R)-rozkład wielkości ziaren. Rysunek 1.1: Kinematyczna teoria dyfrakcji (k.t.d.). Jej rdzeniem jest równanie interferencyjne (lewa gałąź). Rozwinięcie wzoru Debye’a (prawa gałąź) pozwala podać równania wiążące mikrostrukturę krystalitów i natężenie rozproszonego na nich promieniowania. Wyprowadzenia odpowiadające części diagramu zakreślonej linią przerywaną przedstawiono w rozdziale 2. Oznaczenia: RDF(r)-funkcja rozkładu radialnego; SD(r; R)-dystrybucja kształtu; GSD(R)-rozkład wielkości ziaren.
Metoda alternatywana. Alternatywnym podejściem do opisu dyfrakcji promieniowania rentgenowskiego jest równanie Debye’a [?]. Równanie to umożliwia podanie dyfraktogramu proszkowego w zakresie kąta pełnego jedynie w oparciu o znajomość rozkładu odległości międzyatomowych w rozpraszającej drobinie. Teoria ta nie wymaga periodyczności sieci krystalicznej, zakłada zaś przypadkową orientację drobiny3 ; ponadto przyjmuje, podobnie jak teoria Lauego, brak ugięć wielokrotnych oraz stałość absorpcji. Założenie dotyczące przypadkowej orientacji drobin (krystalitów) pokrywa się z fizyczną rzeczywistością dyfrakcji proszkowej, będąc zaletą teorii i w niczym nie ograniczając jej ogólności. Korzystając ze wzoru Debye’a dostaje się więc natężenie promieniowania rozproszonego na proszku złożonym z identycznych drobin o dowolnym kształcie. Na początku lat czterdziestych ubiegłego wieku Stokes i Wilson podali związek pomiędzy szerokością integralną linii bragowskich a pewną funkcją, obliczaną jako objętość części wspólnej krystalitu i jego własnej kopii (“ducha” lub “cienia” krystalitu, ang. shadow) przesuniętej względem oryginału w kierunku rozpraszania [?]. Korzystają oni z własności tej funkcji chociaż, jak piszą, “nie jest łatwo dostrzec jej fizyczne znaczenie”. W latach pięćdziesiątych i sześćdziesiątych XX-go wieku opublikowano prace wiążące transformatę furierowską profilu linii dyfrakcyjnej z funkcją Stokesa i Wilsona [?, str.41][?][?]. Guinier pisze o tej funkcji, że “wykazuje własności analogiczne do funkcji będącej transformatą Fouriera profili linii Debye’a-Scherrera poszerzonych w efekcie małego rozmiaru kryształu (Bertaut [?])” oraz że “nie ma (ona) intuicyjnego związku z formą drobiny” [?, str.12]. W latach późniejszych, korzystając z własności transformaty funkcji Stokesa i Wilsona, obliczono profile linii dyfrakcyjnych dla krystalitów o niektórych kształtach (np. [?][?]). Zawartość pracy. Analiza mikrostruktury nanoproszków węglika krzemu, azotku galu i diamentu o rozmiarach ziaren od 3 do 30nm przeprowadzona w niniejszej pracy, wymagała rozszerzonego podejścia teoretycznego. W pracy udało się rozwinąć tradycyjną teorię Debye’a oraz połączyć ją z podejściem Stokesa i Wilsona oraz Bertaut i Guinier. Rozwijając równanie Debye’a dla periodycznej sieci krystalicznej udało się wyprowadzić, bez jakichkolwiek dodatkowych założeń, dokładne wyrażenia wiążące kształt i rozmiar (nano)krystalitów z profilem linii dyfrakcyjnej proszków bez- i polidyspersyjnych, przy czym rolę funkcji Stokesa i Wilsona pełni w tym podejściu dystrybucja kształtu kryształu, posiadająca przejrzystą interpretację fizyczną. Praca składa się z czterech rozdziałów. W rozdziale 1 przedstawiono wybrane informacje na temat nanomateriałów (nanomateriały, mikrostruktura, ceramiki) z szerszym omówieniem SiC, GaN i diamentu (struktura najgęstszego upakowania, politypia i błędy ułożenia). Opisano też układy eksperymentalne używane w badanich mikrostruktury przedstawionych w niniejszej pracy. W rozdziale 2 przedstawiono rozszerzoną wersję równania Debye’a (zakreślona część diagramu przedstawionego na rys. 1.1 wskazuje schematycznie na rolę jaką ono pełni oraz na jego możliwe zastosowania). Rozszerzenie polega na uwzględnieniu periodyczności sieci krystalicznej nanokryształów. Równanie Debye’a dla kryształów rozdziela się w naturalny sposób na dwie niezależne części: strukturalną i mikrostrukturalną. Pierwsza opisuje kryształ idealny czyli nieskończoną, periodyczną sieć atomów. Druga część, zwana dystrybucją kształtu, zawiera pełną informację jaką dyfrakcja niesie o kształcie i rozmiarze rozpraszającego krystalitu. Zatem dystrybucja kształtu stanowi kluczowy element rozszerzonego równania Debye’a. Znajomość jej postaci analitycznej oraz roli jaką pełni w opisie dyfrakcji pozwala wyprowadzić ścisłe wyrażenia na profile proszkowych linii dyfrakcyjnych. W pracy niniejszej wyprowadzono wzory na profile linii dyfrakcyjnych dla kryształów w formie graniastosłupa i kuli oraz odpowiednie stałe Scherrera. Oprócz tego podano wzór opisujący profil maksimum dyfrakcyjnego realnie istniejących w przyrodzie proszków z rozkładem wielkości ziaren. Analiza wyznaczonego profilu linii dyfrakcyjnej dla proszków pozwoliła podać granice stosowalności metody oznaczania rozmiarów krystalitów z równania Scherrera jak również rozkładu ich wielkości metodą Warrena-Averbacha. W pracy zaproponowano metodę określania rozkładu wielkości ziaren na podstawie szerokości linii dyfrakcyjnej mierzonej na Opracowane metody zastosowano w rozdziale ?? do analizy mikrostruktur nanoproszków węglika krzemu, azotku galu i diamentu o ziarnach od 3 do 30nm. Przedstawiono interpretację fizyczną wielkości otrzymywanych metodą Warrena-Averbacha dla proszków bez- i polidyspersyjnych. Ponadto wyniki analizy mikrostruktury otrzymane z rozpraszania szerokokątowego promieni X porównano z wynikami badań tych samych materiałów badanych daświadczalnie metodą rozpraszania niskokątowego (SAS). W rozdziale ?? zebrano i podsumowano wyniki prac teoretycznych i doświadczalnych uzyskane w ramach niniejszej rozprawy. * Ostatnio, niezależnie od niniejszej pracy, Scardi i Leoni ([?, IX.2001] i [?, III.2002]) oraz Popa i Balzar [?, VI.2002] otrzymali wyrażenia na profil linii dyfrakcyjnej proszku z rozkładem wielkości ziaren. Zawierają one funkcje specjalne4 , które w praktyce ograniczają zastosowania publikowanych wzorów do dopasowań numerycznych. Autor tej pracy pracował nad tym samym problemem, z tym, że rozwiązał go i wyrażenie na profil linii dyfrakcyjnej proszku polidyspersyjnego prezentowane jest w postaci funkcji elementarnych. Właśnie ten wzór oraz wyniki jego dalszych przekształceń są kluczowym elementem pracy. Równoległa praca przynajmniej trzech grup nad tym samym tematem wskazuje, że jest on aktualny i ważny5 . |
| Auxiliary resources (full texts, presentations, posters, etc.) |
|
| Legal notice |
|
| Related papers |
Presentation: PhD Thesis at NANO Ceramics and Grain Boundaries Lab, by Roman PielaszekSee On-line Journal of NANO Ceramics and Grain Boundaries Lab Submitted: 2004-02-24 18:41 Revised: 2011-09-03 02:29 |